
Understanding the ways in which materials deform and develop stresses and how they respond to those stresses is relevant both to biological as well as nonliving systems, including lithium-ion batteries, other semiconducting devices and alloys used for structural applications, such as automobiles, aircraft and buildings. Chemistry, too, plays a role, impacting both living and nonliving systems in important—but not yet fully understood—ways.
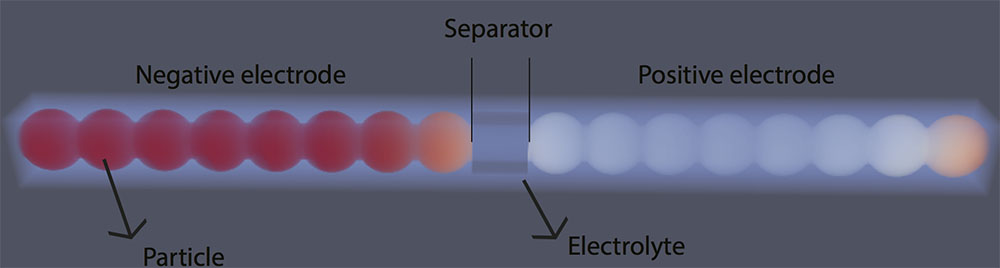
“Chemistry affects mechanics, and mechanics affect chemistry,” said ME Professor Krishna Garikipati, who also holds an appointment in mathematics. Intercalation, the process of atoms being inserted between atomic planes in a crystal lattice, in lithium-ion batteries clearly demonstrates his point.
“Every time we charge our phones, lithium atoms lodge themselves in the battery’s crystal structure and cause it to swell. This happens over and over as we charge and discharge the battery. Eventually, the battery develops microscopic cracks that degrade its ability to hold a charge. There’s a lot of electrochemistry taking place that contributes to the material’s mechanical failure,” he said.
In biological systems, Garikipati’s work at the intersection of mechanics and chemistry—as well as mathematics and physics—has recently focused on patterning and morphology, or the study of form, size, structure and positioning in living systems. Spots on a butterfly’s wings, the patterns on a leopard’s or snake’s skin, precisely where a wing protrudes from an insect’s thorax—we see countless examples every day.
How biological systems sense size and position, both critical to patterning and three-dimensional development, is a central question in the field of developmental biology.
Take eye color, for example. “In order for cells in the iris to be able to implement the developmental blueprints contained in their chromosomes, they need to know where they are so that they develop the right features—color, for instance—at the right size in the right place,” Garikipati explained.
So how are size and position determined? Cells carry genetic instructions in their DNA, and the process by which DNA is transcribed to produce proteins that carry out specific functions is increasingly well understood. But these processes alone don’t tell the whole story.
Scientist and mathematician Alan Turing’s reaction-diffusion equations describe many patterning phenomena, and some mass transport equations do, too. More recently, biophysicists are recognizing that physical forces, governed by nonlinear elasticity, also play key roles in determining size and positioning.
In an article published in the Journal of the Mechanics and Physics of Solids in 2017, Garikipati presented an overview of the partial differential equations that govern patterning and morphogenesis observed by developmental biologists.
He notes that research into the two phenomena of patterning and morphogenesis has taken place, to a great extent, independently of one other. The theoretical frameworks he has developed, by contrast, attempt to bridge the physical processes by focusing on the corresponding equation systems.
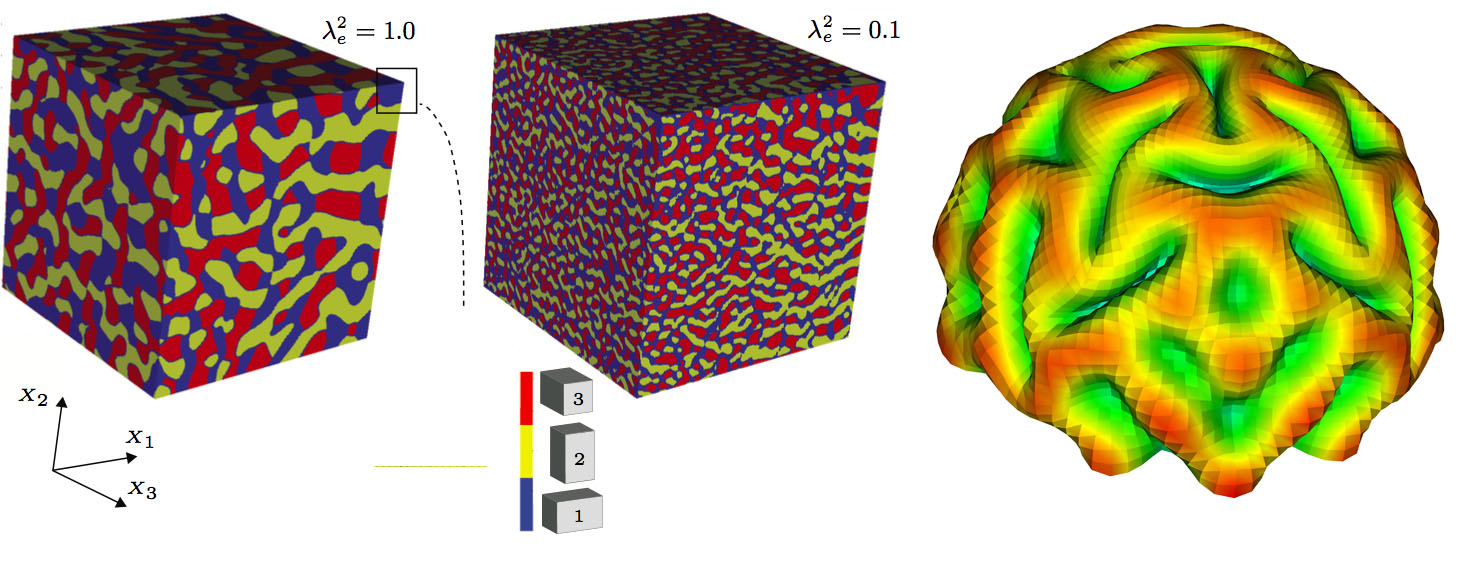
Theoretical frameworks in hand, Garikipati works closely with biologists to take these mathematical and physical descriptions and apply the equations developed to a range of questions, including how villi form in the small intestine and how the folded pattern of the brain’s cortex is created.
“That foldedness serves a neurological purpose; it’s not just a curiosity,” Garkipati said. The increased surface area created by the ridges (gyri) and the grooves (sulci) allows neurons to be situated close to each other. As a result, the axons that connect them don’t have to build as lengthy a path and instead can develop more complex connections.
“If the gyri and sulci don’t fold—or buckle, to borrow an elasticity term—like they’re supposed to, or they’re not the right size or in the right position, developmental abnormalities ensue,” Garikipati said. “Bringing mechanics theories to bear helps us better describe how healthy and unhealthy folding occurs.”
In related work, published in Integrative Biology in 2016, Garikipati and colleagues created a novel predictive computational model describing how tissue forces and signaling events interact to very quickly create the patterns in cell membranes that determine where each villus should be positioned.
While the general role of mechanics had been suspected for a few years, Garikipati’s work showed that a particularly intricate choreography of cell multiplication, migration and forces of cell contractility underlies the early stages of villi formation and positioning.
MACHINE LEARNING TO PREDICT PHYSICS
The next step, in both biological and materials systems, is to put the new theoretical models through their paces in an ambitious data-driven computational initiative, which leverages the latest advances in machine learning, or artificial intelligence. “We’ve validated our models experimentally, so we know we’ve incorporated the right physics. Turning to data now will help us fill in some of the details about values and parameters that aren’t settled by theory alone,” said Garikipati, who also directs the Michigan Institute for Computational Discovery & Engineering. “New methods in machine learning will help use big data to improve our capability to model and predict physics.”
